How To Sample From A Univariate Gaussian
In yesterday’s post, I explained inverse transform sampling, a sampling technique which uses the quantile function to sample from a desired distribution. But there was a bit of an issue that I glossed over: it assumed that the quantile function itself is efficiently computable! Thankfully, for the case of the exponential distribution, this wasn’t an issue as the quantile function only involves taking a logarithm.
(How exactly computers compute logarithms, I don’t know. But we will simply take it on faith that there are efficient algorithms for computing elementary functions like exponentials, logarithms, etc.)
But consider the normal distribution—a standard probability distribution if there ever was one. We know that for the standard normal distribution, it has a PDF of the form:
\[g(x) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}}\]Clearly, at any given point $x$, we can calculate the PDF at $x$ using only elementary operations/functions (in this case, squaring and exponentiation). But what about the CDF? The standard expression for the CDF $\Phi$ of the normal distribution is
\[\Phi(x) = \frac{1}{\sqrt{2 \pi}}\int_{-\infty}^x \ dt \ e^{-\frac{t^2}{2}}\]Well, this is disappointingly circular. The CDF of the normal distribution is…the function that you get when you integrate the PDF of the normal distribution.
Unfortunately, while I’m pretty sure that that the derivative of an elementary function is always elementary, it’s not the case that the antiderivative of an elementary function is always another elementary function. There is no closed-form expression for the CDF of the normal distribution in terms of recognizable “simple” functions.
(If this seems odd, consider the fact that $\pi$—or any other transcedental number—can’t be expressed in terms of rational numbers by way of a finite application of addition, multiplication, and taking radicals.)
So what do we do?
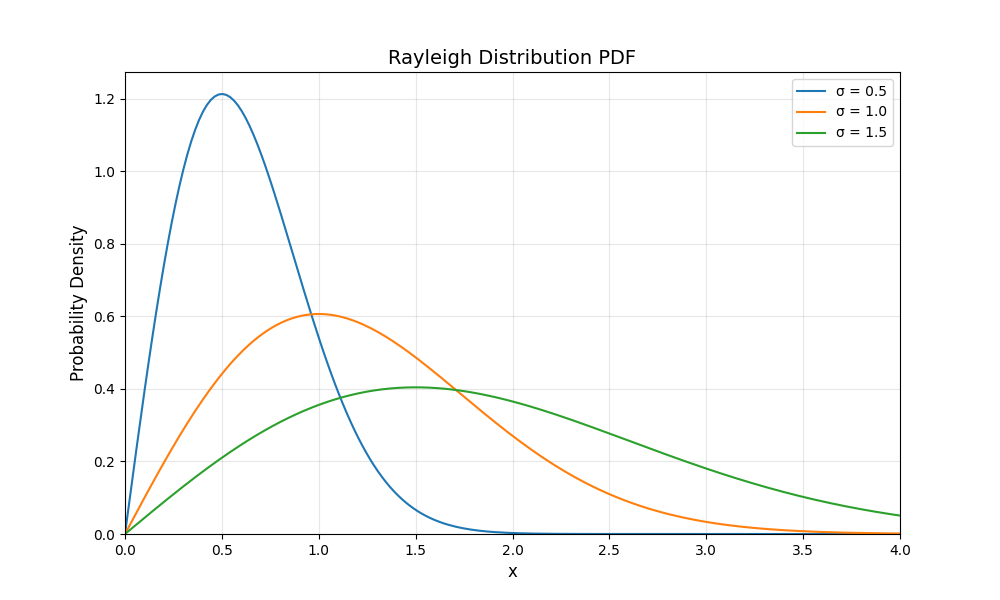
Well, while we can’t find a closed-form expression for the CDF of the normal distribution, we can find a closed-form expression for the anti-derivative of $f(x) = x e^{-\frac{x^2}{2}}$—which, at least superficially, seems like a closely-related distribution.
Using the substitution $u = \frac{t^2}{2}$, we have that the CDF $F$ of our new distribution is:
\[\begin{align} F(x) &= \int_0^{x} dt \ t e^{-\frac{t^2}{2}} \\ &= \int du \ e^{-u} \\ &= - \Big|_{0}^{x} \ e^{-\frac{t^2}{2}} \\ &= 1 - e^{-\frac{x^2}{2}} \end{align}\]And that our quantile function is
\[F^{-1}(x) = \sqrt{2 \ln \frac{1}{1 - x}}\]As desired, the quantile function $F^{-1}$ can be expressed as the composition of elementary functions. Therefore, we can sample from $f$ using inverse transform sampling.
So how does this help us? Our new distribution $f$ is called the Rayleigh distribution. The Rayleigh distribution, among other things, models the speed of a free gas molecule that is confined to two-dimensions.
Let’s take a quick detour into some statistical physics to see why this is the case.
Given a physical system in contact with a temperature bath, the distribution of microstates of the system is given by the Boltzmann distribution. The Boltzmann distribution gives a probability density of the form:
\[p(\mathbf{x}) \propto e^{-\beta H(\mathbf{x})}\]where $\mathbf{x}$ is phase space coordinates of the system, $H$ is the Hamiltonian of the system, and $\beta$ is thermodynamic beta.
We have a non-interacting gas in two-dimensions, so $H = \frac{1}{2} m (v_x^2 + v_y^2)$. Our Hamiltonian only has a kinetic term as there’s no potential energy term for non-interacting particles.
For simplicity, let’s set $m$ and $\beta$ equal to one. So our joint probability density function for $v_x$ and $v_y$ has the form:
\[p(v_x, v_y) \propto e^{-\frac{(v_x^2 + v_y^2)}{2}}\]Note that both $v_x$ and $v_y$ are normally-distributed random variables. That will be important later.
For now, what we want is not the joint probability distribution for the velocities, but the probability distribution for the speed $s = \sqrt{v_x^2 + v_y^2}$. To do so, we will change variables from $(v_x, v_y) \rightarrow (s, \phi)$ where $\phi$ is the angle (WLOG) with respect to the x-axis. When performing a change of variables, the probability density is multiplied by the determinant of the Jacobian:
\[p_{s,\phi}(s, \phi) = p_{v_x,v_y}(v_x(s,\phi), v_y(s,\phi)) \cdot \left | \det \left(\frac{\partial(v_x, v_y)}{\partial (s, \phi)}\right) \right |\]Our Jacobian determinant is:
\[\begin{align} \left | \det \left(\frac{\partial(v_x, v_y)}{\partial (s, \phi)}\right) \right | &= \left|\begin{vmatrix} \frac{\partial v_x}{\partial s} & \frac{\partial v_x}{\partial \phi} \\ \frac{\partial v_y}{\partial s} & \frac{\partial v_y}{\partial \phi} \end{vmatrix}\right| \\ &= \left|\begin{vmatrix} \cos(\phi) & -s\sin(\phi) \\ \sin(\phi) & s\cos(\phi) \end{vmatrix}\right| \\ &= s\cos^2 \phi + s\sin^2 \phi \\ &= s \end{align}\]So we have that
\[p_{s,\phi}(s, \phi) \propto s e^{-\frac{s^2}{2}}\]We have rotational invariance, so we can marginalize out $\phi$ and the overall shape of the distribution remains the same. We then have that
\[\hat{p}(s) \propto s e^{-\frac{s^2}{2}}\]which shows that the speed $s$ is indeed Rayleigh-distributed as claimed. We can then use the fact that the individual components of the velocity $v_x$ and $v_y$ are related to the speed $s$ in the following way:
\[v_x = s \cos \phi \quad \text{and} \quad v_y = s \sin \phi\]$s$ is Rayleigh-distributed and $\phi$ is uniformally-distributed. We know how to sample from both of these distributions using inverse transform sampling. If we plug in our sampled value for $s$ and our sampled value for $\phi$ into the above formulas, we will get simultaneous samples for $v_x$ and $v_y$—which are both normally-distributed quantities.
But wait: We know that $\cos^2 \phi + \sin^2 \phi = 1$. So wouldn’t there be some statistical dependency between the realized values of $v_x$ and $v_y$?
No. It is true that conditional on a particular value of $s$, $v_x$ and $v_y$ are indeed not independent.
\[p(v_x, v_y|s) \neq p(v_x|s) p(v_x|s)\]But for the unconditioned distribution, before you’ve determined your value for $s$, $v_x$ and $v_y$ are independent.
\[\begin{align} p(v_x, v_y) &\propto e^{-\frac{(v_x^2 + v_y^2)}{2}} \\ &= e^{-\frac{v_x^2}{2}} e^{-\frac{v_y^2}{2}} \\ &\propto p(v_x) p(v_y) \end{align}\]So to recap: using two independent samples $u_1$ and $u_2$ from the uniform distribution on $[0,1]$, we can produce two independent and samples $x_1$ and $x_2$ from the standard normal distribution. The procedure is:
- Apply the quantile function of our Rayleigh distribution to the first uniform sample $u_1$ to get the sample value for the speed: $s = F^{-1}(u_1)$.
- Multiply the other uniform sample $u_2$ by $2 \pi$ to get a sample for the angle $\phi$.
- Use the equations $x_1 = s \cos \phi$ and $x_2 = s \sin \phi$ to get two independent samples from the normal distribution.