'Field Guide to Probability Distributions' by Gavin Crooks

My first intellectual obsession was Pokémon. I watched the animated television show religiously and played Pokémon Silver on my Game Boy Advance SP until the late hours of the night.

That’s a pretty typical childhood for someone of my generation. Pokémon is the largest grossing media franchise in the world. It spans video games, TV shows, movies, trading card games, action figures, and more.

The reason why Pokémon is so popular is that it taps into our childlike need to collect. “Gotta catch ‘em all!” isn’t just a catchy marketing slogan, but gets at the very heart of the ethos of Pokémon. Children are instinctively curious about the natural world around them; without any encouragement, children categorize the different species of flora and fauna that they encounter.

In my case, not only was I obsessed with Pokémon, but I was also obsessed with Animal Planet and books about species of Old World monkeys and apes. And the creator of Pokémon got the idea for the franchise from his boyhood hobby of collecting bugs, a popular pastime among boys in Japan (which is also why Bug Catcher is such a common class of trainer in the Pokémon universe).

I’ve since moved on from Pokémon. The last Pokémon game I played was Pokémon Ultra Sun near the end of high school. After one slow cutscene too many, I called it quits. (Though I still watch competitive Pokémon on YouTube.)

But the boyhood impulse to collect is still there. Just channeled into different forms. When I started to get into statistical physics and probability theory in undergrad, I started “collecting” different probability distributions. Just like how different Pokémon have different types, stats and abilities, the different (parametric families of) probability distributions have different characteristics: their domain of definition, the number of parameters that describe the family, the common physical situations where they arise, their relationship to other probability distributions, etc. Wikipedia was helpful for this as it has a page listing various probability distributions organized by their support. When I was bored in class, I would just load the Wikipedia page and read about some obscure distribution that arises in population ecology, fascinated by its high-level characteristics and curious if I would ever encounter a situation where just that distribution might come in handy.

The problem with the Wikipedia page, however, is a lack of structure. Sure, it organizes the distributions by their domain of support. But what’s fascinating about probability distributions is that they are interconnected in various ways. Some distributions are special cases of other distributions. There are often algebraic relationships between distributions. For example, the chi-squared distribution arises from the sum of squares of independent, identically distributed (iid) standard normal random variables.

I thought it would be cool to have a side project where I create a Pokédex for probability distributions: rather than just cataloguing them in one place, I create a comprehensive go-to encyclopedia for understanding the world of probability distributions.

It turns out that Gavin Crooks already beat me to the punch.

The Structure of the Book

Gavin Crooks is a chemist, well-known for his work on non-equilibrium statistical mechanics and thermodynamics. His most famous contribution is the Crooks fluctuation theorem. Despite being a chemist by training, his work is easy to parse for someone like me who comes from a physics background—which is not always the case when trying to understand how someone with a different background approaches subjects that I am nominally familiar with. (In the past, I’ve leafed through some work that labelled itself as “chemical thermodynamics”—usually involves lots of $\Delta G$ calculations of various reactions—and I’ve had a hard time understanding what was going on.)

After a decade and a half publishing cutting-edge results in non-equilibrium statistical mechanics, Crooks decided to write the book Field Guide to Probability Distributions. The book is a brisk walk through many of the most common probability distributions that you will find in mathematics, statistics, physics, and engineering. Here is the family tree of probability distributions featured in the book:

The tree is structured so that more general distributions are near the top and more specific distributions are near the bottom. Daughter nodes are special cases of their parent nodes. Imagining each parametric family of probability distributions as forming a statistical manifold, special cases correspond to submanifolds. These submanifolds can be obtained by fixing one or more parameters to specific values, establishing relationships between parameters, or taking limits of parameters.

For example, consider the family of power function distributions:

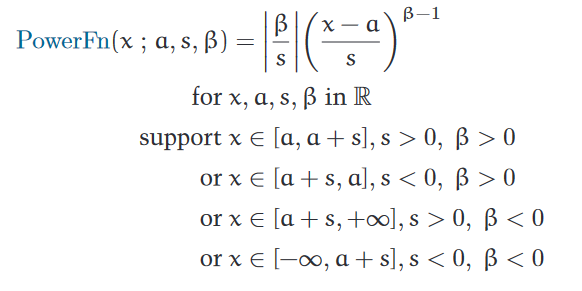
This family is exactly what it sounds like: the parametric family of probability distributions which follow some power law. It has three parameters, including a power parameter $\beta$. If you take the special case when $\beta = 1$, the overall exponent in the probability density function becomes 0, causing the density to be constant on the domain of the distribution. This is precisely the two-parameter family of uniform distributions.

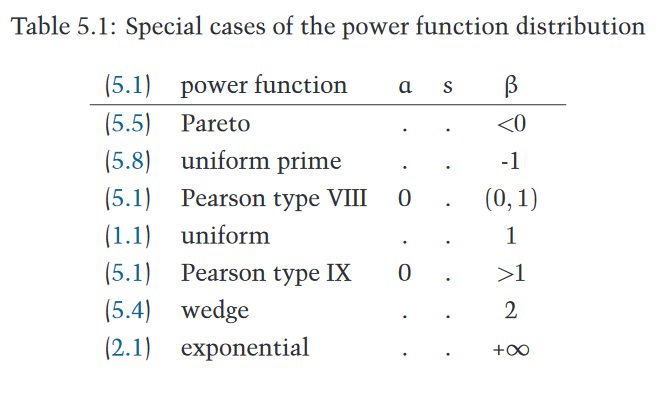
This informs the structure of the book. Rather than starting with the most general distributions, the book actually starts with the bottom nodes of the tree. These are familiar distributions like the uniform distribution, the normal distribution, and the exponential distribution. The book then considers more and more general distributions, making sure to spend time connecting them back to the more specific distributions that were introduced earlier in the book.

Each mini-chapter provides handy statistics about each distribution, including the values of its moments expressed as functions of the parameters, common alternative parameterizations, and other names the distribution goes by. (Most of the probability distributions in this book have many aliases due to being rediscovered in various contexts.)

One of the strong points of this book is that it uses consistent notation. For example, scale parameters which appear in distributions as diverse as the uniform distribution and the beta distribution are often denoted as $s$. Or how location parameters are usually denoted as $a$. Small little consistency checks like this do a lot for helping to understand the connections being made.

There are a couple choices of notation that I couldn’t quite parse. For example, when parametrizing the Amoroso distribution (and its special cases like the Gamma distribution), instead of denoting the scale parameter with $s$, Crooks instead opts for $\theta$. I assume there is a good reason for this—whether it’s conceptual or conventional, I don’t know.

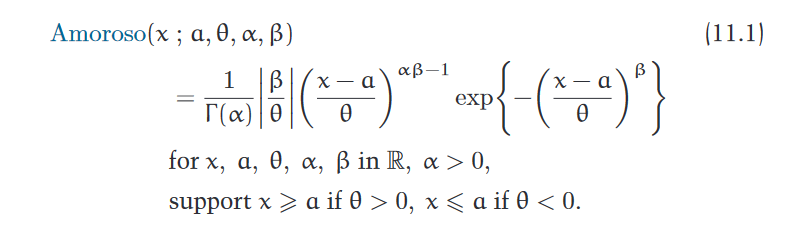
In any case, the book has a table in one of the appendices that lists the physical interpretation of each parameter.

This book restricts itself to continuous, univariate probability distributions. This is a prudent choice due to the hierarchical structure of the book. While there are often connections between discrete and continuous probability distributions, these relationships can’t be neatly codified using the hierarchical structure that the book adopts. Discrete distributions also have a different flavor to them: they lean more heavily on various contexts from combinatorics. As for multivariate distributions, those are much too complicated, as you need to specify not only the marginals but also the potentially complex correlations between the individual random variables.

The Grand Unified Distribution

At the very top of the tree is the Grand Unified Distribution (GUD) which encompasses every other distribution in the book as a special case:

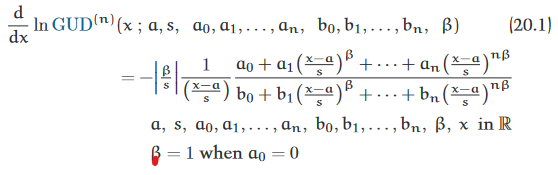
It’s asserted by Crooks that every analytic probability distribution is the solution of this differential equation for some values of the parameters. More interestingly, he conjectures that most “interesting” distributions (which I interpret to mean those distributions that naturally arise in mathematical and physical contexts) satisfy this differential equation for low-order (degree 2 polynomials) in the numerator and denominator.

It’s been a couple of months since I first read the book, but I still haven’t fully grasped what the GUD is trying to tell me. On the surface, it reminds me of exponential families. However, while exponential families focus on moments and cumulants of the random variable (and therefore, expectation values of polynomials), the GUD seems to extend beyond polynomials to consider rational expressions. Or at least, that’s my best guess. Writing this paragraph has made me realize that I don’t understand exponential families as well as I should.

Maybe it will help to work through an example. Given the standard normal distribution, it satisfies the differential equation:

\[\frac{d}{dx} \log p(x) = -x\]

One key observation: for any given set of parameter values, the local extrema (maxima or minima) of the probability density function correspond to the zeros of the polynomial featured in the differential equation. This suggests that the normal distribution might be considered the “simplest” distribution with a mode, as it’s characterized by a first-degree polynomial in this differential equation.

But if the zeroes of the rational expression correspond to local extrema, how should I interpret the poles?

Anyways, this feels like a topic for a future blog post.

Useful Stuff for Probability Theorists

After the main section of the book concludes, there are several appendices that are quite useful in their own right.

First, Crooks lists some miscellaneous distributions that didn’t fit into the hierarchical structure of the book. These include the family of stable distributions (distributions which are closed under addition of random variables):

And personal favorites like the Voigt distribution (the convolution of a Gaussian and a Lorentzian):

There is also a nice appendix on order statistics:

Many of the distributions covered in the main section of the book are actually the distributions of order statistics of more well-known distributions.

Lastly, there is an appendix on the algebra of random variables. A lot of it was review (such as how addition of independent random variables corresponds to the convolution of their probability density functions). But some of it was novel to me (like the section on functions of random variables).