Phase Transitions As Global Optimization

If I had to boil down phase transitions to their essence, it would be this: phase transitions result from thermodynamic systems being solvers of global optimization problems. All of the weirdness involving phase transitions—why they are so hard to work with formally—arises because while local optimization ideas are ubiquitous in physics, global optimization ideas are relatively confined to statistical mechanics (at least, at the undergraduate/early-graduate level).

This phase-transition-as-global-optimization perspective is not new. In a statistical field theory class, you will often encounter integrals like this one:

\[Z = \int \ dx \ e^{-N \beta L(x)}\]

This is the familiar expression for the partition function as the sum of Boltzmann factors with some added physical assumptions. ($L$ is often meant to represent a sort of free energy density rather than the Hamiltonian.)

The standard way to handle these sorts of integrals is Laplace’s method. One can use Laplace’s method when (a) you have an integral where the integrand is an exponential and (b) there is some large term in front of the exponent. In this case, that large term is $N$—which represents the number of microscopic degrees of freedom of the system. In the limit of large $N$, we can approximate the integral as a Gaussian integral about the global minima of the function $L$.

\[\begin{align*} \int dx \ e^{-N\beta L} &\approx \int dx \ e^{-N \beta (L(x_\text{min}) + \frac{1}{2} L''(x_\text{min})(x- x_\text{min})^2)} \\ &= e^{-N \beta L(x_\text{min})} \sqrt{\frac{2 \pi}{N \beta L''(x_\text{min})}} \end{align*}\]

These sorts of large $N$ limits are often called “taking the thermodynamic limit”. That Laplace’s method requires expanding about the global minima will be emphasized in any half-decent exposition on the technique. But I still think the conceptual leap from working with global versus local optima is underemphasized relative to its importance. I would say that pretty much all the difficulty in grokking phase transitions and solving related homework problems comes from physics students having developed tools and intuitions for understanding the behavior of systems about local minima, but lacking a similarly well-developed arsenal for analyzing global minima. It doesn’t help that, as far as I’m aware, this toolset doesn’t really exist.

As presented in standard statistical mechanics textbooks, the central dilemma of phase transitions is: how does one get non-analytic behavior (e.g., discontinuous changes in the magnetization of a magnet) from the microscopic laws of physics—which are, as far as we know, completely analytic? The standard physical answer is that non-analyticity comes from taking the thermodynamic limit. The partition function is the sum of Boltzmann factors for each of the different states of the system. These Boltzmann factors, being exponentials, are analytic functions of thermodynamic variables. For any finite system, the finite sum of these analytic Boltzmann factors would lead to an analytic partition function. But the infinite sum of analytic functions can be non-analytic. It’s the process of taking this infinite sum that allows phase transitions to happen.

This perspective is both true and insightful. But for me, thinking in terms of partition functions is a bit too unwieldy. I can nod my head at the force of the argument, but I can’t quite visualize what the phase transition looks like in my head. What has made phase transitions click for me is the perspective provided by Landau theory, where the system performs a global optimization of the order parameter to minimize its free energy.

Trying to derive Landau theory from first principles would be taking us too far astray, but let me try to motivate the basics.

The Second Law of Thermodynamics says that entropy increases over time. In a closed system, this leads to the system being in the maximum entropy state, consistent with conserved quantities (e.g., the amount of energy). When a system is no longer closed, but can exchange energy with the environment, this picture becomes a bit more complicated. What wants to be maximized is the entropy of the entire universe, not just the entropy of the small little slice of the universe that we decided to consider.

It’s also true that, all else being equal, the more energy a system has, the higher its entropy. Entropy is the amount of information required to fully specify the microstate of the system, given the macrostate. Consider a gas: higher energy means that the gas molecules are moving faster. If you imagine the distribution in momentum space, keeping speed constant you have a sphere of possible velocities compatible with that speed. The larger the speed, the larger the surface area of the sphere, and thus the larger the entropy of the gas.

So there is a sense in which energy is a currency with which a system can maximize its entropy. However, energy is conserved: if the system has some unit of energy, that’s one less unit of energy for the rest of the universe to use to maximize its entropy. This presents a tradeoff: the system wants to simultaneously maximize its entropy and minimize its energy. (And temperature is precisely what quantifies which point on this entropy-versus-energy tradeoff curve is optimal.) This motivates the free energy:

\[F = U - TS\]

The dual objective of maximizing entropy and minimizing energy is thus turned into the single objective of minimizing the free energy.

Thermodynamic systems are global minimizers of free energy: they will arrange themselves (while obeying their underlying physical constraints) in whatever way minimizes free energy given the external physical conditions (e.g., temperature, pressure, external magnetic field, etc.). Because the free energy is composed of two competing objectives, this opens the door for different strategies. The main axis along which strategies can differ is ordered versus disordered. Systems that employ a strategy of minimizing their energy are ordered systems. When a lattice of spins are all aligned, its energy is minimized and the system is ordered. Systems that employ a strategy of maximizing their entropy are disordered systems. When the lattice of spins is in random arrangements, its entropy is maximized and the system is disordered.

It is helpful to quantify what strategy the system is employing using what is called an order parameter. As its name suggests, the order parameter of a system quantifies how ordered it is: it is usually taken to be zero in disordered phases and non-zero in ordered phases. What best constitutes an order parameter will depend on the system in question. For magnetic systems, the order parameter is the magnetization: the average value of the spins in the lattice. Assuming there is no external magnetic field, in the disordered phase, the net magnetization is zero. In the ordered phase, the net magnetization will be some non-zero quantity.

We’re almost there. Landau theory is a framework for analyzing thermodynamic systems which can be briefly summarized by the following assumptions:

1. The thermodynamic state of the system can be represented using an order parameter.
2. The free energy density is an analytic function of the order parameter.
3. The coefficients of the Taylor expansion of the free energy density with respect to the order parameter are analytic functions of thermodynamic variables.
4. Thermodynamic systems will inhabit the state (value of the order parameter) which globally minimizes their free energy density.

Assumptions 2 and 3 are crucial, but also subtle and the hardest to justify. I won’t even try to justify them here. But taking them as given, the elegance of Landau theory is that it compresses all of the non-analyticity into one single step—the step of finding the global minimum. Everything else about the setup is purely analytic. Consider the following graph of the free energy density versus the order parameter:

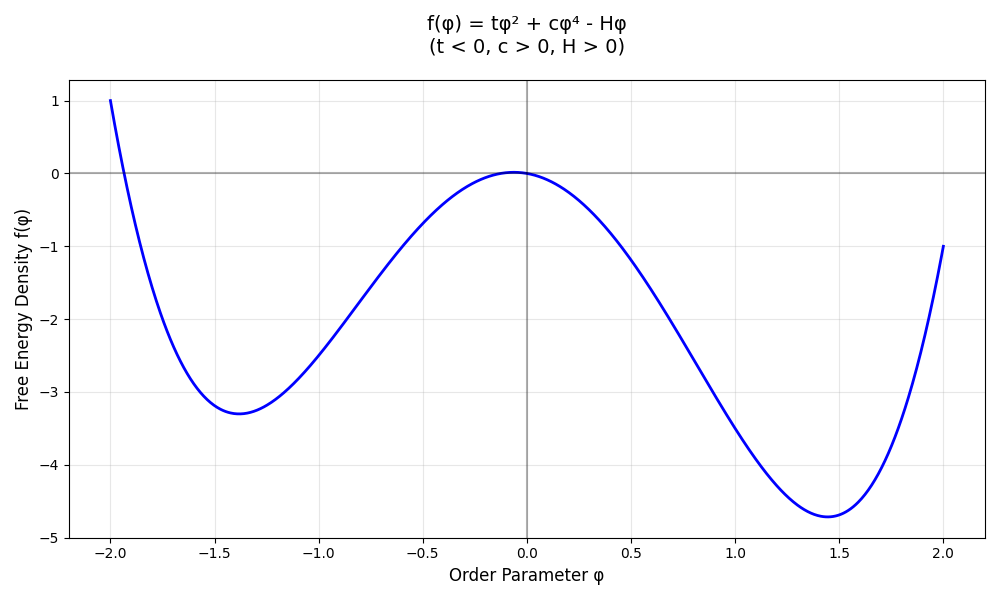
This graph shows a typical free energy curve for a ferromagnetic system (a magnetic system that maintains non-zero magnetization even in the absence of a magnetic field). Here the linear term in $\phi$ represents the coupling of the lattice to an external magnetic field. We can clearly visualize the phase transition as we vary the sign of the magnetic field. When $H > 0$, the global minimum is to the right. When $H = 0$, there are two global minima symmetric about the y-axis. And when $H < 0$, there is a global minimum to the left. This discontinuous change in the location of the global minimum is precisely the phase transition.

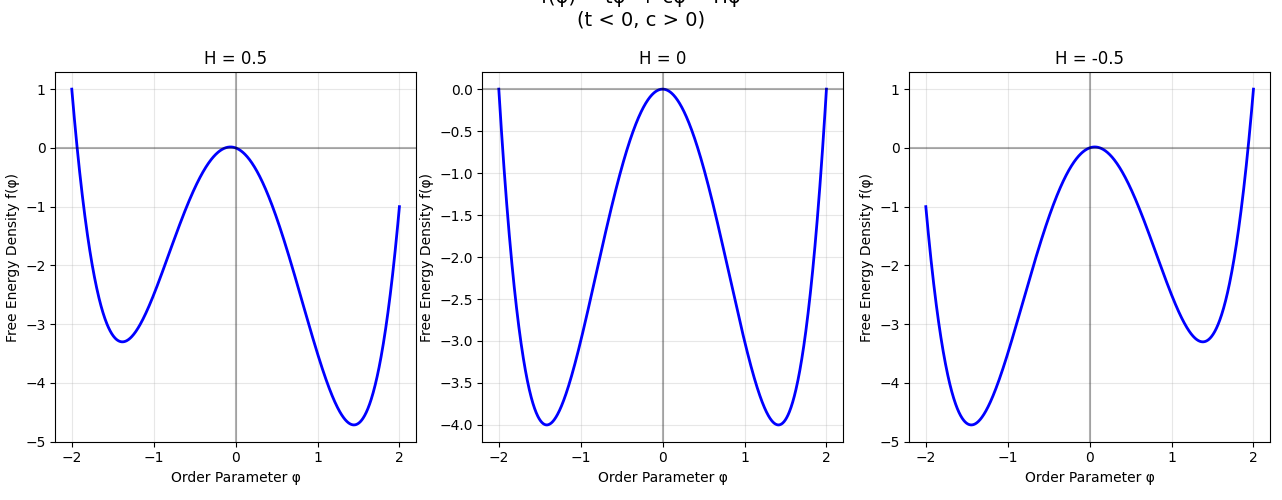
To recap, the following is true in Landau theory:

1. Keeping the coefficients constant, the free energy density is an analytic function of the order parameter. Therefore, small changes to a strategy correspond to well-behaved small changes in the attained free energy density.

2. Keeping the order parameter constant, the free energy density at that value of the order paramter changes analytically with small changes in the coefficients (which are assumed to be analytic functions of the thermodynamic variables). To visualize this, imagine staying at one order parameter $\phi_0$ as we change the external $H$ field. The free energy density $f(\phi_0; H)$ will change analytically as we change $H$. This is true at all values of $\phi$. The “success” of a strategy will change in a small, well-behaved way if there is a small change in the external conditions.

3. The value of the global minimum of the free energy density is a continuous (though not necessarily analytic) function of small changes in the coefficients. Even at a phase transition, there is no discontinuity in global minimum of the free energy. The intuition is that phase transitions are precisely when the free energy of two competing strategies “cross”.

4. The argmin of the free energy density (the value of the order parameter that corresponds to the global minimum) can not only change non-analytically, but it can also be discontinuous with respect to small changes in external parameters. (In an advanced statistical mechanics course, you will study phase transitions where the argmin changes continuously but in a non-analytic fashion—these are called continuous phase transitions for this reason.)

A key thing to emphasize is that phase transitions always arise from non-analytic behavior in the argmin with respect to the external parameters. I would go as far as to say that this constitutes a definition of what a phase transition is.

What I like about the “Phase Transition as Global Optimization” framework is its generality. Phase transitions that we see in other areas of science—not just in physics—can be neatly conceptualized in this way. For example, I think economics is a particularly good area to consider phase transitions. In economics, rather than studying thermodynamic systems minimizing free energy, you might be analyzing firms maximizing profits or agents maximizing utility. And rather than performing global optimization over the order parameter, it might be global optimization over the allocation of some scarce resource (e.g., a firm has to optimize over how much to spend on labor versus capital).

Despite the superficial differences, the analogy is quite strong—and somewhat oddly, considering my physics background, when trying to play with phase transitions intuitively in my head, I lean on economic metaphors about as often as I do physical ones. (This is why I’ve been using the somewhat unorthodox anthropomorphic language of “strategy” throughout this post.)

For fun, let’s consider the problem of deciding what to study in college. For simplicity, imagine this is a world where there are only two subjects: English and Math. And students choose what to study based on what will maximize their career earnings.

We can plot the time spent studying English and Math versus expected lifetime income. The coefficients of the curve are arbitrarily complicated functions of all the various internal and external factors that must be considered when choosing one’s career (including personal attributes like talent and motivation as well as external factors like the prevailing market conditions).

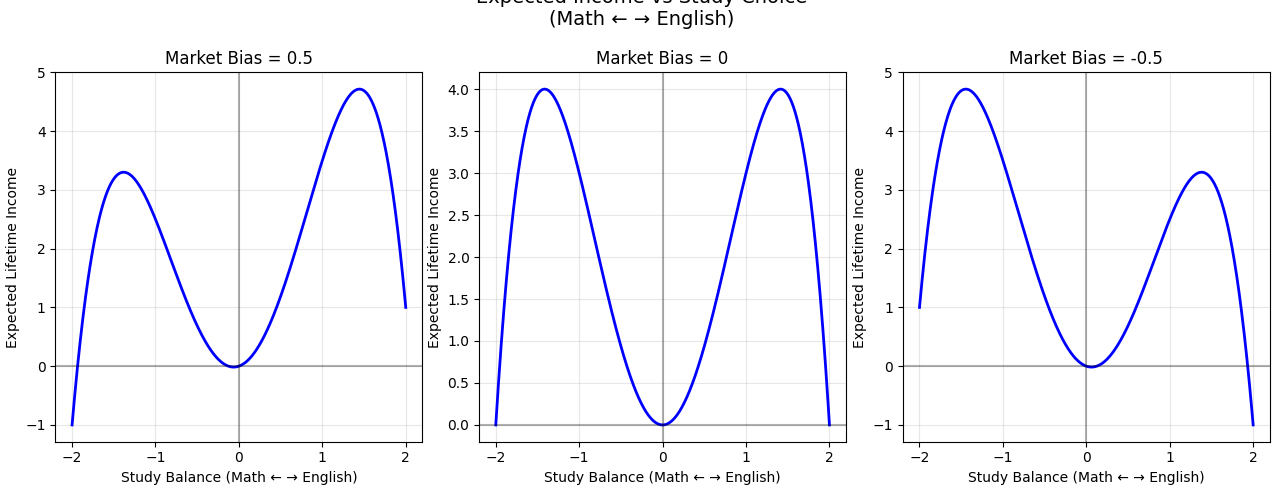
(The punchline of course is that this is the earlier plot of magnetization-versus-free-energy turned upside-down.)

What I like about this economic perspective is that it highlights how phases emerge from the benefits of specialization. When I set up the analogy, I didn’t assume the existence of majors, yet the plot still shows this multi-modality. It seems intuitive that it’s more economically viable to take Calculus III and Differential Equations or Creative Writing and Literary Analysis than Calculus III and Creative Writing. Similarly, a ferromagnetic system faces the choice between “specializing” in spin-up or spin-down. Specialization appears to be a recurring pattern across reality—whether in physics, economics, or ecology.

In the examples I considered in this post, the space of possible strategies was compressed into one dimension (whether it was net magnetization or English-versus-math studying time). But in real life, the space of possible tradeoffs is high-dimensional with many peaks and valleys. There isn’t just English versus Math. There’s lawyer versus doctor versus engineer versus chemical engineer versus pulp and paper engineer versus tissue paper process engineer.

We often talk about strategies not as continuous, but as discrete. For this discrete notion of strategies, I would define them as modes in the space of whatever value function we are trying to extremize. Phase transitions arise from this multimodality.