Detailed Balance Explained
Alternative Title: Detailed Balance Is Just Chain Rule
A Markov chain is a system where the probability distribution of the next state depends solely on the current state, not on the past history. The chain is said to obey detailed balance if, at equilibrium, any sequence of states is equally probable when run forwards or backwards—meaning the system’s dynamics look the same in either time direction. To illustrate this condition, consider the following two Markov chains, both defined on a triangle graph:
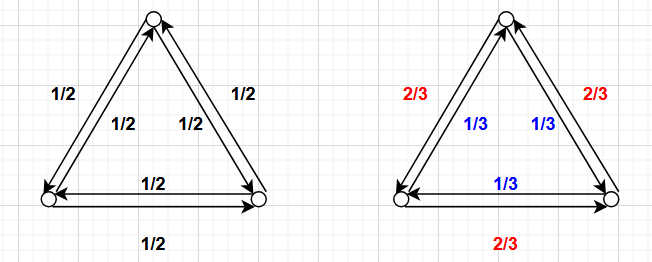
The Markov chain on the left is reversible—it satisfies detailed balance. As we have equal probability of going counterclockwise and clockwise, there is no way to distinguish probabilistically between a given sequence and its reversed sequence. But the chain on the right is irreversible. It doesn’t satisfy detailed balance. For any given sequence, if we count the number of counterclockwise versus clockwise moves, we can make inferences about its direction in time. If there are more counterclockwise moves than clockwise moves, the sequence is more likely to be moving forward in time. If there are more clockwise moves than counterclockwise moves, then our best guess is that the chain is moving backwards in time. (With these Markov chains, any given sequence is possible in both forward and backward time, so it’s impossible to know for sure which direction time is moving—we can only talk about the relative probabilities.)
Let $P_{ij}$ be the probability that, conditional on being in state $i$, we transition to state $j$ in the next time step. The probabilities ${P_{ij}}$ form a matrix $P$ called the transition matrix. For the above two Markov chains, their respective transition matrices (denoted $P_1$ for the left chain and $P_2$ for the right chain) are:
\[P_1 = \begin{pmatrix} 0 & 1/2 & 1/2 \\ 1/2 & 0 & 1/2 \\ 1/2 & 1/2 & 0 \end{pmatrix}, \quad P_2 = \begin{pmatrix} 0 & 2/3 & 1/3 \\ 1/3 & 0 & 2/3 \\ 2/3 & 1/3 & 0 \end{pmatrix}\]A couple things to keep in mind about transition matrices:
-
All entries must be between 0 and 1 as they are probabilities.
-
The ith row is the conditional probability distribution of the next state given an initial state of $i$. Therefore, the rows (but not the columns) must sum to 1.
-
It is conventional in linear algebra for vectors to be represented as column vectors which matrices act on from the left (e.g., $Ax = y$). However, because in Markov chains the initial state corresponds to the row index and the final state corresponds to the column index, probability distributions are represented as row vectors which multiply the matrix from the left (e.g., $xP = y$).
Associated with a given Markov chain is its steady state distribution. There are two ways to conceptually think about steady states. In one picture, you have an atom that moves indeterministically according to the probabilities prescribed by the chain. Imagine this task: the atom starts at some position (let’s say the top vertex) and then I put a blindfold on you while the chain moves forward $t$ time steps. Even though the atom is still a single atom, since you can’t see it, you must describe your knowledge as a probability distribution. At first, your probability distribution changes rapidly—you know it started at the top, but you become less and less sure of its location. Over time, your distribution barely changes, as the initial information you had before the blindfold was put on becomes exponentially irrelevant. The distribution that your beliefs asymptote to is the steady state of the Markov chain.
A different, equivalent perspective is that you have a fluid of total volume 1 and the graph represents a water system where the nodes are wells and the edges are aqueducts. The fluid represents a probability density over vertices of the graph. At each time step, the Markov chain tells you what fraction of the fluid at each node to send to its neighbors. Eventually, after a long time, the amount of fluid a given node sends out becomes exactly equal to the amount of fluid it receives. The steady state distribution tells you the fraction of the total fluid in each node.
(It’s important to note that not all Markov chains have steady state distributions. But we won’t worry about that for now.)
Let $\pi$ denote the steady state distribution. The steady state distribution is the fixed point of the transition matrix $P$: the steady state distribution doesn’t change over time. This is equivalent to the steady state distribution being a (left) eigenvector of the transition matrix with an eigenvalue of 1:
\[\pi P = \pi\]By inspection, one can see that, despite one chain being reversible and the other being irreversible, both chains have the same steady state distribution:
\[\pi = \begin{pmatrix} 1/3 & 1/3 & 1/3 \end{pmatrix}\]Now that we’ve defined both the transition matrix $P$ and the steady state $\pi$, we are finally in a position to give a precise statement of detailed balance. A Markov chain satisfies detailed balance if the following condition holds:
\[\pi_i P_{ij} = \pi_j P_{ji}\]for all pairs of states $i$ and $j$.
To understand where this condition comes from, let’s briefly introduce a notation for talking about sequences of states.
Let $i_n$ represent the proposition “being in state $i$ at position $n$ in the sequence.” For example, $j_2$ means “being in state $j$ at position 2.” Using this notation, we can write the detailed balance condition for any pair of states $i$ and $j$ as:
\[p(i_1, j_2) = p(j_1, i_2)\]This equation says something quite intuitive: the probability of being at state $i$ in the first time step and then at state $j$ in the second time step must equal the probability of being at state $j$ first and then at state $i$.
Using the chain rule, we can decompose each of these joint probabilities:
\[p(i_1)p(j_2|i_1) = p(j_1)p(i_2|j_1)\]As we mentioned before, detailed balance is a property of Markov chain that is obeyed at equilibrium. At steady state, the marginal probabilities are given by the stationary distribution $\pi$, and the conditional probabilities are entries of the transition matrix $P$. So in terms of our previous notation: we have that $p(i_1) = \pi_i$, $p(j_1) = \pi_j$, $p(j_2|i_1) = P_{ij}$, and $p(i_2|j_1) = P_{ji}$. That means we can write the above equation as:
\[\pi_i P_{ij} = \pi_j P_{ji}\]which is precisely the detailed balance condition!
In general, it seems important to be able to interpret transition matrices/kernels as conditional probability densities—and vice versa. I’ve seen this intuition be load-bearing in a couple of different places, most notably when deriving the Kolgomorov forward equation. This is important in this case because it explains why the naive definition of detailed balance—that the transition matrix $P$ is symmetric—is not correct. We care about symmetry between the joint probabilities, not the conditional probabilities.
A way to think about detailed balance is that it captures the notion of being locally at equilibrium. If we return to our analogy of imagining the system as containing fluids with wells and aqueducts, we said that steady state corresponds to when, for each node, the total fluid it sends out equals the total fluid it receives. Detailed balance corresponds to a more stringent condition: rather than just requiring that the total flows in and out match, we now require that for each pair of states, the fluid flowing from one to the other equals the fluid flowing in the reverse direction.
Mathematically, detailed balance encodes pairwise stationarity. Consider a transition matrix $P$. For any two states $i$ and $j$, we can examine the dynamics isolated to that subsystem. For both Markov chains defined above, let’s analyze the subgraph consisting of just the two vertices at the bottom of the triangle.
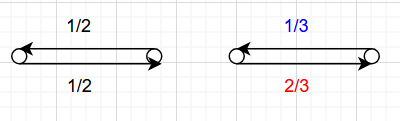
To obtain the transition matrix $P’$ for this subsystem, we must follow this procedure:
- Extract the $2 \times 2$ submatrix corresponding to the subsystem
- Renormalize each row by adding to the diagonal entries until each row sums to 1 (This makes our chain “lazy”)
If our original system satisfies detailed balance, then the steady state of any subsystem will have probabilities in the same ratio as the probabilities of those states in the original system. (Reminder: steady states correspond to left eigenvectors!)
In our two systems above, we get subgraph transition matrices (denoted $P_1’$ and $P_2’$) of:
\[P_1' = \begin{bmatrix} 1/2 & 1/2 \\ 1/2 & 1/2 \end{bmatrix}, \quad P_2' = \begin{bmatrix} 1/3 & 2/3 \\ 1/3 & 2/3 \end{bmatrix}\]For $P_1’$, the steady state is $(1/2, 1/2)$—which has the same ratio as in the original chain. But for $P_2’$, corresponding to our irreversible system, we have a steady state of $(1/3, 2/3)$. The two vertices are not locally in equilibrium with each other.
One last thing: an important property of detailed balance is that it holds for sequences of arbitrary length. However, it turns out that if your Markov chain is reversible for length-2 sequences, then it will be reversible for length-$n$ sequences. To prove this, we can proceed by induction: we will show that if a Markov chain has reversible $n$-sequences, this implies that all $(n+1)$-sequences are also reversible.
Assume that $n$-sequences are reversible where $n \ge 2$, meaning for any states $a, b, …, k$:
\[p(a_1, b_2, ..., j_n) = p(j_1, ..., b_{n-1}, a_n)\]Let $(a_1,…,k_{n+1})$ be an $(n+1)$-sequence. Then using the chain rule:
\[p(a_1,...,k_{n+1}) = p(a_1,...,j_n) \times p(k_{n+1}|a_1,...,j_n)\]But because we have the Markov condition, we can simplify the conditional probability to only depend on the last state:
\[p(a_1,...,k_{n+1}) = p(a_1,... ,j_n) \times p(k_{n+1}|j_n)\]A couple things to keep in mind before we present the full proof:
- As we have $n$-sequence detailed balance, we also have 2-sequence detailed balance. By 2-sequence detailed balance, we know $p(j_n)p(k_{n+1}|j_n) = p(k_{n})p(j_{n+1}|k_n)$ for any pair of states $j$ and $k$.
- Because we are at steady state, we have time-translation symmetry for all marginals, conditionals, and joint probabilities with respect to location in the sequence. For any integers $m,n$, we have $p(i_n) = p(i_m)$, $p(j_{n+1}|i_n) = p(j_{m+1}|i_m)$, and $p(a_{1 + m},…, j_{n+m}) = p(a_1,…, j_{n})$
We can then show that:
\[\begin{align*} p(a_1,\cdots,k_{n+1}) &= p(a_1,\cdots ,j_n) \times p(k_{n+1}|j_n) \quad &\text{ (chain rule)} \\ &= p(j_1,\cdots ,a_n) \times p(k_{n+1}|j_n) \quad &\text{ (inductive hypothesis)} \\ &= [p(j_1) p(i_2|j_1)\cdots p(a_n|b_{n-1})] \times p(k_{n+1}|j_n) \quad &\text{ (chain rule)} \\ &= [p(i_2|j_1) \cdots p(a_n|b_{n-1})] \times p(k_{n+1}|j_n)p(j_n) \quad &\text{ (time translation)} \\ &= [p(i_2|j_1) \cdots p(a_n|b_{n-1})] \times p(j_{n+1}|k_n)p(k_n) \quad &\text{ (detailed balance)} \\ &= [p(k_1) p(j_2|k_1) p(i_3|j_2) \cdots p(a_{n+1}|b_n)] \quad &\text{ (time translation)} \\ &= p(k_1,j_2, \cdots ,a_{n+1}) \quad &\text{ (chain rule)} \end{align*}\]Thus showing the $(n+1)$-sequence is also reversible.