A Physical Analogy for the Jensen-Shannon Divergence
The current professor that I am working with seemingly knows everything about sampling despite being roughly the same age as me. That’s why, on the rare occasions where I know something that he doesn’t, I’m always caught off-guard.
During our most recent weekly meeting, I was talking to him about what I had been up to in the past week. A good portion of my time had been spent chipping away at the six hundred pages of reading that he’d generously recommended to me in our previous meeting. But I’d also spent some time reading about non-equilibrium statistical mechanics. Non-equilibrium statistical mechanics is one of those subjects that I keep revisiting, but have never been able to quite conquer—either due to a lack of mathematical maturity or perhaps due to lacking some crucial bit of physical intuition.
A very helpful post-doc recommended this review article by Christopher Jarzynski that does a good job going over the basics. The article covers major fluctuation theorems (including Jarzynski’s equality and Crooks fluctuation theorem) and discusses ways to quantify the irreversibility of a thermodynamic process. (You can think of processes as trajectories in space of thermodynamic coordinates.) One approach to quantifying irreversibility is to measure the work dissipated during a process. Another approach is to quantify how much the distribution of forward trajectories of microstates differs from the distribution of backward trajectories of microstates for the reversed process.
(For an example of a non-equilibrium process, imagine moving a piston wall in a finite time. During compression, air bunches up against the wall. During decompression, the space near the moving wall becomes empty. This asymmetry is what we aim to quantify.)
I was explaining all this to the professor. And then I said, “One way to quantify the difference between the distribution of forward and backwards trajectories is the Jensen-Shannon divergence.” And he was like, “What’s that?”
As I’ve mentioned before, there are two “problems” with the KL divergence as a probability metric.
- If $p$ is not absolutely continuous with respect to $q$, then $\text{KL}(p||q)$ is infinite.
- The KL divergence is asymmetric: $\text{KL}(p||q) \neq \text{KL}(q||p)$.
The Jensen-Shannon divergence is what I would consider to be the most obvious way to solve both of these problems. It’s defined as
\[\text{JS}(p||q) = \frac{\text{KL}(p||m) + \text{KL}(q||m)}{2}\]where $m$ is the mixture measure $m = \frac{p + q}{2}$.
A measure $p$ is absolutely continuous with respect to $q$ if whenever $q$ assigns zero probability to a set, $p$ must also assign zero probability to that set. In other words, $p$ can’t put probability mass where $q$ has none. This might seem like a reasonable constraint, but it causes problems in practice because if $p$ puts any probability mass where $q$ has none, then $\text{KL}(p||q)$ blows up to infinity.
The Jensen-Shannon divergence addresses this by introducing a mixture measure $m = \frac{p + q}{2}$. Think about what this means: for any measurable set $A$, if $p$ assigns it probability $p(A)$, then $m$ will assign it at least $\frac{p(A)}{2}$. Similarly, if $q$ assigns probability $q(A)$ to a set, then $m$ assigns at least $\frac{q(A)}{2}$.
This guarantees that both $p$ and $q$ are absolutely continuous with respect to $m$! Because if $m$ assigns zero probability to a set, that means both $p$ and $q$ must assign zero probability to that set. We never get into a situation where $p$ or $q$ are trying to put probability mass where $m$ has none. So both $\text{KL}(p||m)$ and $\text{KL}(q||m)$ are guaranteed to be finite.
The symmetry part then follows naturally from the definition—we’re just averaging $\text{KL}(p||m)$ and $\text{KL}(q||m)$, so of course $\text{JS}(p||q) = \text{JS}(q||p)$.
A natural follow-up question: In what physical context does the Jensen-Shannon divergence naturally arise?
The answer that I originally came up with was: imagine you have a cylinder partitioned into two parts. Instead of considering the thermodynamic entropy (which is an extensive quantity—a quantity that scales with the size of the system), let’s consider the entropy per unit volume. Let’s say we quantify that entropy per unit volume based on the distribution of speeds of the gas molecules in each part, call them $p$ and $q$. If you release the partition, then the Jensen-Shannon divergence measures the entropy produced by the mixing.
I felt pretty satisfied with this analogy when I came up with it. But on reflection, it’s fundamentally wrong. Here’s why: Let’s say that two distributions of gas molecules differ in their distribution of velocities because they are at different temperatures. Then when you lift the partition, the distribution of gas molecules would settle on the Maxwell-Boltzmann distribution corresponding to the averaged temperature—which is not the same thing as the mixture measure $m = \frac{p + q}{2}$.
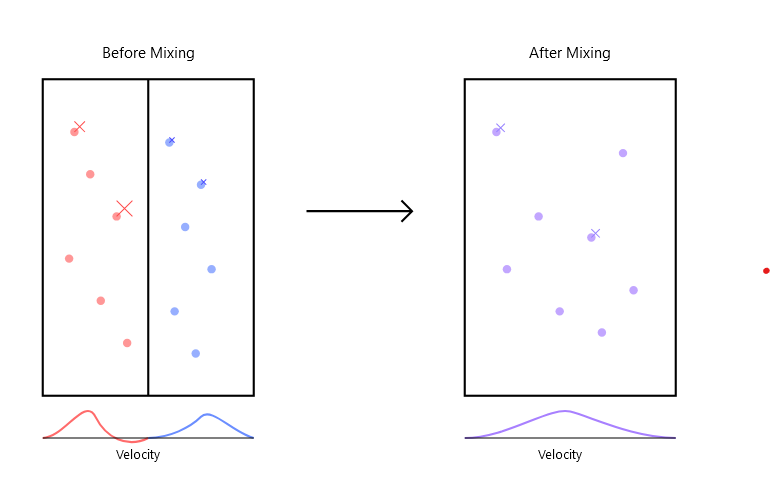
The analogy above would only really work if the gases from both sides of the partition couldn’t interact with each other when mixed. But then you might as well come up with a different analogy entirely.
So here’s an attempt at that different analogy.
Imagine that in some town there are two hotel conferences: one for dwarves and one for elves. The dwarves are on average fairly short, befitting their ground-dwelling, blacksmithing way of life. And the elves are tall as befitting their tree-dwelling, archery-focused way of life. You could talk about the entropy in the distribution of heights at each conference.
Then, imagine if there is some natural disaster (a typhoon) that destroys both of the hotels. So the conferences have to be combined. The distribution of heights would then be exactly the mixture measure, since dwarves remain dwarves and elves remain elves—they don’t suddenly average their heights just because they’re in the same conference hall.
The key seems to be that Jensen-Shannon divergence seems to measure the entropy production (increase in uncertainty) when you have mixing without “interaction”. How common is this physically? I can keep coming up with constructed examples (e.g imagine you have two urns filled with pebbles with different distributions of weights and you mix them), but I am scratching my head a bit about natural situations where the Jensen-Shannon divergence emerges as the distance measure of choice. It apparently comes up in generative adversarial networks, but I don’t think in that context it’s the unique choice dictated by the structure of the problem.