You Should Read Andrew Gelman
I came into my PhD with the expectation of specializing in biophysics. But after a year and a half, I’ve now switched to working with a statistics professor on physics-inspired sampling algorithms. This might seem like a sudden mid-PhD pivot, but I’ve actually been interested in statistics—not statistical physics, but statistics—for many years now.
While it’s hard to pin down exactly when I became interested in statistics, I’m pretty sure that my first introduction to academic statistics was through the work of Andrew Gelman. Gelman is a renowned statistician at Columbia who has contributed to many areas of both theoretical and applied statistics.
Gelman is a truly prolific blogger. As far as I can tell, he’s blogged daily for over twenty years—all while continuing to publish books, research articles, teach classes, and travel for conferences. He’s so organized and productive that he is able to schedule out blog posts months in advance. I have no idea how he does it.
He is best known for his work in Bayesian statistics. Bayesian statistics is a theory of statistics where probabilities are interpreted to represent subjective beliefs. The foundation of Bayesian statistics is a simple but powerful formula called Bayes theorem that tells you how to update your subjective probability of an event happening when receiving new information. It’s given by the following formula:
\[P(A|B) = \frac{P(B|A)}{P(B)}P(A)\]At its core, statistics is the study of how to draw conclusions from data. Frequentist statistics is the default paradigm—it’s basically the statistics that you would learn in an undergrad social science methods class. Its foundations were laid by early 20th century statisticians, most notably R.A. Fisher, who established how statistics should be applied in the sciences.
Bayesian statistics offers a different approach. Its key feature is that you have to specify a prior— a mathematical representation of your beliefs before you perform the experiment. This fundamental difference between Bayesian and frequentist approaches has sparked debates that go back decades. Fisher and Harold Jeffreys engaged in particularly acrimonious debates over these methods.
Gelman has talked at length about the Bayesian versus frequentist debate. While he’s ultimately a Bayesian, he is even-keeled and gives both sides their due. His writing shows that the philosophical questions underpinning our statistical methods matter because they guide how we use statistics in practice. Through his blog, Gelman demonstrates that many mistakes social scientists make come from an insufficient understanding of the assumptions and circumstances under which their statistical tools are applicable.
Starting in the 2000s, there was a replication crisis in the social sciences. When other researchers attempted to reproduce many famous studies—especially in psychology—they couldn’t replicate the original findings. The foundations of several academic fields were shaken overnight.
At first, it was a trickle. One paper here. One retraction there. But soon the trickle became a downpour. So people naturally started asking questions: How did this happen? How can we stop a replication crisis from ever happening again?
There are many social and scientific reasons underpinning the replication crisis. But one key contributer was the misuse of statistics. And Gelman was one of the leading voices pointing out instances of statistical malpractice and giving advice for what researchers can do to avoid falling into the most common traps.
For example, he popularized the phrase “garden of forking paths” (lifted from a Borges short story). Due to the publish-or-perish culture in academia, researchers feel pressure to report experimental results that are publishable. Too often, “publishable” is determined by whether the main finding is significant—where “significant” can be understood both in the technical statistical sense of p-values and in the colloquial sense of appearing important.
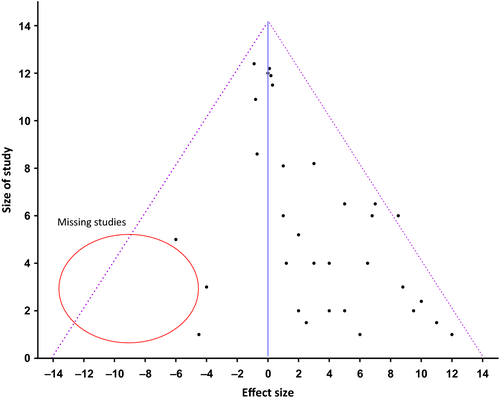
When performing experiments, there will inevitably be spurious correlations: statistical relationships between variables that arise from sampling/experimental noise rather than robust underlying relationships. Researchers can test many different relationships and only report those that meet the required significance threshold. This distorts the meaning of the reported statistics, which assume no such selection effects are occurring (to properly interpret the p-values, one would need to control for multiple hypothesis testing).

This led to him advocating for solutions like pre-registration. With pre-registration, experimenters must explain their intended experimental design and specify which relationships they want to study before conducting the experiment. Pre-registration has slowly been adopted by different research groups, though it’s far from widespread. It requires an unusually clear understanding of the experimental design and relevant questions—it essentially removes the “exploratory” step which is traditionally a major part of science.
If I had to summarize Gelman’s work, it’s about the inseparability of theoretical and applied statistics. Theoretical statistics is crucial for understanding the assumptions underlying our statistical tools—this understanding allows us to use them properly and recognize when to be skeptical of their results. Applied statistics is equally crucial, as researchers’ practical mistakes when using statistical tools can guide us toward better statistical frameworks for conducting science. Or as he would put it: theoretical statistics is the theory of applied statistics.
This is also how I understand his Bayesianism. Critics of Bayesianism often question where the prior comes from. But advocates like Gelman argue that we are always working with a prior. Even in frequentist statistics, we’re making implicit prior assumptions. The strength of Bayesian statistics is that all of our assumptions are explicit and above board, rather than hidden in the methods.