Are Dissertations Underrated?
When trying to master a new subfield, there can be a bit of gap in resources.
If you are completely new to a subfield, then you will want to consult textbooks. Good selections of textbooks can be found in many places online like niche subreddits or on StackExchange threads. Once you’ve compiled a list of textbooks, you can download them off websites like libgen or Anna’s Archive and peruse them, selecting the ones that best suit your style and current level of ability.
(To be clear, I don’t use libgen or Anna’s Archive as that would be in violation of the copyright law of the United States of America and associated territories. But I have friends who do and they can attest to their usefulness.)
If you are an expert, then you can read papers. These will often be the papers of collaborators or competitors: people whose work that you have been tracking continuously. Because you have been staying up to date, you aren’t lacking in relevant context and even little idiosyncracies like personal preferences in notation will be familiar to you.
But what if you are a graduate student who is trying to get up to speed so that you can start to contribute novel results? Sure, at the beginning, you will be reading the hardest, most technical graduate-level monographs. But often, there will be a decade gap between the most recently-published textbook and the current state-of-the-art in the field. This is exacerbated if you are working in a currently-trendy subfield—which, almost by definition, is a situation that most graduate students find themselves in.
Of course, graduate students aren’t going at it alone. One of the primary responsibilities of your advisor is to address this exact problem. But it would still be nice to be able to take your education into your own hands. Maybe because your advisor is unusually hands-off. Or maybe because your specific project is just outside of your advisor’s core expertise, such that they aren’t familiar with the best review articles and they can’t just personally teach you the relevant ideas during your regularly scheduled meetings.
One solution to this problem that I’ve found has been in the most unexpected of places: PhD dissertations. This is unexpected because everyone jokes that dissertations are meant to be written, not meant to be read. And the citation counts attest to this: even for relatively popular researchers, their dissertations will have middling citations (probably because dissertations are often compilations of the research papers that the student wrote during the course of their PhD—so one would just cite the original paper.)
Here is a personal example. I’ve been busy learning about sampling. And one of the guiding principles in our little fiefdom of sampling is that sampling is optimization. This slogan can be interpreted at a conceptual level: when sampling, we are optimizing over the space of measures to reach our target distribution. Or it can be interpreted at a more literal and technical level: a lot of the different sampling techniques are just techniques from optimization with Brownian motion slapped on, or they have an optimization counterpart that served as the original inspiration.
This analogy is beautiful. There is one problem: I don’t know anything about optimization! I guess I could go off and read a couple of textbooks to fix that problem. But from afar, optimization seems like a huge field. Where would I even start? What I need is a distillation of the ideas and algorithms from optimization that are most relevant to me.
This dilemna has been lurking in the back of my mind for a while, but I didn’t have any active plan on how I was going to resolve it. But one day, on a lark, I decided to start reading Ashia Wilson’s dissertation on the use of Lyapunov functions in optimization. She attended the recent sampling conference at Yale and is co-authors with Andre Wibisono, so I knew that her work might be of interest to me. As luck would have it, in her dissertation, I found exactly what I was looking for!
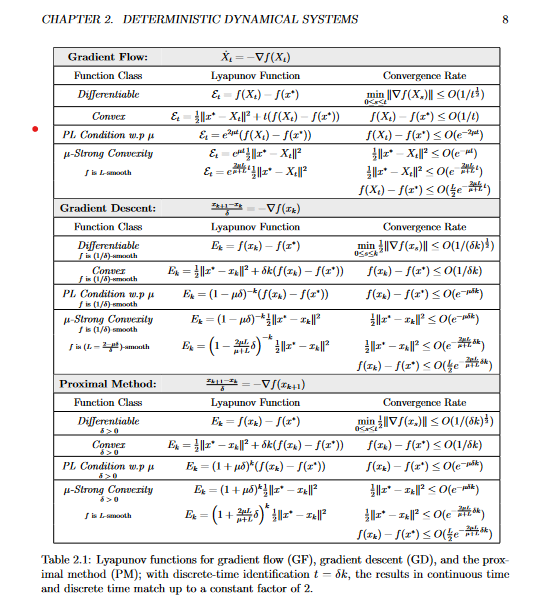
I won’t explain this table (when I finish reading her dissertation, I’ll probably write up a little mini-review), but look at how pedagogical it is! It features some of the most common optimization algorithms under common conditions of the optimization function. This isn’t the type of table you’d typically find in a research paper since there isn’t anything new here. But for my purposes, it’s still incredibly useful.
And this isn’t an isolated instance. I’ve also gotten a lot of value out of reading Gavin Crook’s dissertation and Sinho Chewi’s dissertation. Why would this be?
I think there are two things going on. One is that—due to academic competitive pressures—dissertations are now really long. Part of this phenomenon is attributable to dissertations becoming increasingly niche as science continuously specializes. But part of this is surely that a compact twenty-page dissertation just can’t help but seem less impressive than a 500-page one—even if the amount of new information contained in each is the same. So to pad out the word count, dissertations now contain a lot more background than they used to.
The other contributing factor is the intended audience of the dissertation: your committee. Your committee members will often be working in adjacent subfields but won’t have the deep expertise that active researchers in your area have. So (I suspect) dissertations include so much pedagogy for their sake. But the side effect is that dissertations are built to get someone with a technical background up-to-speed as quickly as possible so they can interpret your work—which, as graduate students, is exactly what we’re looking for!