'Statistical Optimal Transport' by Sinho Chewi

A common problem in statistics is that of sampling. Let’s say we have some unknown distribution $\pi$. We can ask

1. Practically, how do we go about producing samples that “draw” from $\pi$?

2. When can we be sure that our sample sufficiently resembles the true underlying distribution?

Most people’s earliest introduction to sampling is in high school when they learn about introductory statistics concepts like the standard deviation of the mean. The standard deviation of the mean, while simple, is actually a nice illustration of the type of questions that the field of sampling is concerned with.

To recap: Let’s say that you are sampling from some distribution $\pi$. Then given a sample of size $n$, you can compute the sample mean and the sample variance. These are measures of the average values of the points in the sample and how spread out the points in the sample are, respectively.

\[\bar{x} = \frac{1}{n} \sum_{i=1}^n X_i \quad \text{and} \quad s^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{x})^2\]

The standard deviation of the mean (SEM) is a bit different than the sample mean and sample standard deviation. Unlike the latter two quantities, the SEM is not a property of the sample, but a property of the underlying distribution and its distribution of samples. It tells you, given a sample size of $n$, how far (in absolute distance) you should expect the sample mean to be from the true population mean.

\[\text{SEM} = \mathbb{E}_n || \bar{x} - \mu||\]

You could then ask: how does the SEM change with $n$? Intuitively, we know that it should decrease; the larger your sample, the more likely it is that your sample is representive of the population that it was drawn from. But can we quantify this relationship?

Yes. Computing the standard deviation of the mean when drawing from a univariate Gaussian is straightforward and worth computing for yourself. What you will find is that as a function of sample size, the standard deviation of the mean goes asymptotically as $\frac{1}{\sqrt{n}}$.

But the mean is only one property of a probability distribution. If, for example, you have a bimodal distribution as your true distribution, then you are less interested in whether the mean of your sample matches the mean of your population. Instead, you might be more concerned with more complex questions, such as how quickly the relative weights of the two modes in your samples come to resemble the relative weights in the true distribution.

It’s also straightfoward to ask how close the mean of the sample is to the mean of the population. If you have a one-dimensional distribution, then you just find the magnitude of the difference between the means; even if you have a multivariate distribution, you just take the magnitude of the difference of the vector of means. There is a natural, canonical metric structure for $\mathbb{R}^d$.

But it’s less straightforward to ask whether one probability distribution is “close” to another. One common way is via the KL divergence (also known as the cross entropy):

\[\text{KL}(p || q) = \int dp \log \frac{dp}{dq}\]

$\Big (\frac{dp}{dq}$ is something called the Radon derivative. Don’t worry too much about it. For our purposes, $\frac{dp}{dq} \equiv \frac{p(x)}{q(x)}. \Big )$

But the KL divergence has some unsatisfying properties. A big one is that the KL is very sensitive to the relationship between the support of $p$ and the support of $q$. If the coding distribution $q$ is zero on an interval where the true distribution $p$ is non-zero, then the KL divergence is actually infinite. (One can see from the expression for the KL that we would be dividing by zero—which is not good.) Somewhat troublingly, this is not true for the converse. If the coding distribution $q$ is non-zero when the true distribution $p$ is zero, then the KL evaluates to 0 .

\[\lim_{x \rightarrow 0} x \log x \longrightarrow 0\]

The KL divergence is assymetric.

But more to the point: we want to compare the distribution of our sample (which is called the empirical distribution) to the true distribution. However, the empirical distribution is not smooth. It is discrete, composed of Dirac delta functions. The probability density function of the empirical distribution is typically written as:

\[\hat{f}_n(x) = \frac{1}{n} \sum_{i=1}^n \delta(x - X_i)\]

where $\delta$ is the Dirac delta function, $X_i$ are the observed values, and $n$ is the sample size.

Discrete distributions don’t play nicely with the KL divergence. The problem is that the KL divergence is ultimately a vertical distance measure. To compute the distance between two distributions, it takes the ratio between them at each point, takes the log of those ratios, and then sums everything up.

So if there is a single interval where the coding distribution is zero, but the true distribution is non-zero, the KL divergence is infinite. This leads to weird counterintuitive results like if you consider two uniform distributions, both of diameter 1, the KL divergence between them is infinite unless they share the same center (and zero in the case that they do share the same center).

In many common instances, the KL divergence doesn’t match our intuition—which is more continuous. Our intuition is that the uniform distribution on $[0,1]$ is very similiar to the uniform distribution on $[0.1, 1.1]$ and very different from the one defined on $[1000000, 1000001]$. Is there a distance measure that does that?

Yes. It’s called the Wasserstein distance. It comes from a subfield of probability theory called optimal transport. If the KL divergence is a vertical notion of distance, then the Wasserstein distance (and optimal transport in general) is concerned with a more horizontal notion of the distance between probability distributions.

The field has its origin in the Monge problem. Let’s say you have a mound of dirt. And you want to transform that mound of dirt into a differently-shaped mound. And let’s say that cost of transporting a speck of dirt is proportional to both the mass of the speck as well as the distance that the speck travels. You can then ask: What is the smallest possible cost with which you can transport dirt and turn the original mound into the target mound? What does this transport plan look like?

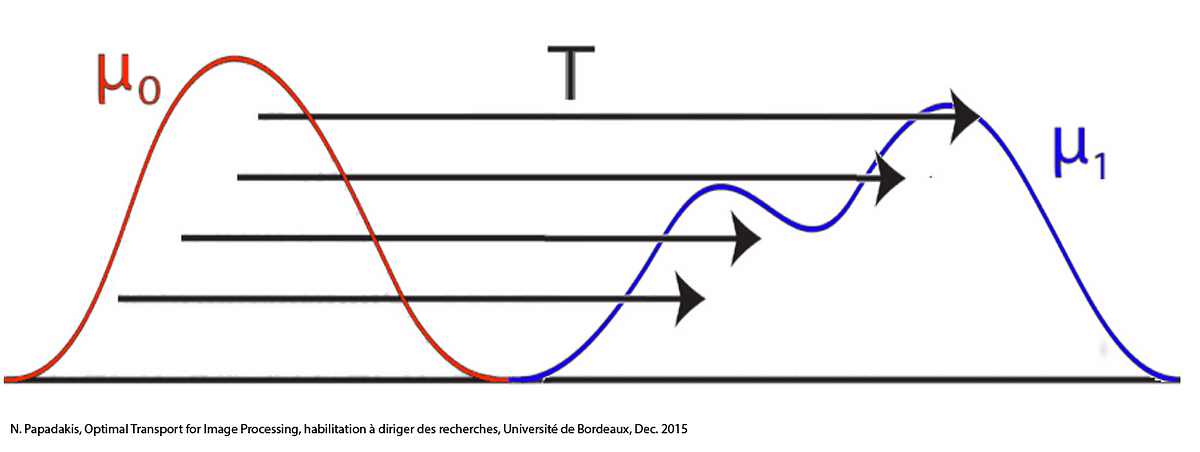
The Monge problem is old, first proposed in the 18th century. The original problem asked for a solution in terms of transport maps. But it turns out that this is too restrictive to be interesting. So the modern formulation of the problem (which we owe to Russian mathematician Kantorovich), instead of using transport maps, instead imagines the two mounds of dirts as probability distributions $\mu$ and $\nu$. And the transport plan is replaced by the optimal coupling $\gamma$. A coupling of two probability distributions $\mu$ and $\nu$ (which we’ll assume are both distributions over $\mathbb{R}^d$) is a joint probability distribution over $\mathbb{R}^d \times \mathbb{R}^d$ whose $x$ and $y$ marginals are $\mu$ and $\nu$. We can denote $\Gamma(\mu, \nu)$ to be the set of all couplings of $\mu$ and $\nu$.

The Wasserstein distance is the minimal expected distance achieved by the optimal coupling:

\[W(\mu, \nu) = \inf_{\gamma \in \Gamma(\mu, \nu)} \int |x-y| \gamma(dx, dy)\]

This notion of distance is better. It’s symmetric: $W(\mu, \nu) = W(\nu, \mu)$. And one can show that it satisfies the triangle inequality. It meets the mathematical requirements of a metric.

The Wasserstein distance is also much better behaved when working with distributions of dissimilar supports, such as when working with discrete and continuous distributions simultaneously. It also doesn’t diverge. The Wasserstein distance between any two probability measures is always finite.

Because we have a notion of distance between probability measures that behaves well with both discrete and continuous distributions, we can now ask questions like: given a distribution $\mu$ and the random empirical distribution $\mu_n$, what is the expected Wasserstein distance as a function of $n$.

\[\mathbb{E} \left[ W(\mu, \mu_n)\right]\]

This is the field of statistical optimal transport.

Optimal Transport

This book is meant to be an introduction to the field of statistical optimal transport. It requires a good bit of mathematical maturity (I would peg the book as a first-year grad level text), but it assumes surprisingly little background. You will want to understand probability theory at an undergrad level (for example, be comfortable with marginals), but otherwise, the book teaches a lot of the other math it uses in a clear, albeit somewhat brisk manner.

The first four chapters of the book introduce optimal transport and briefly discuss some of the most common problems studied in optimal transport theory.

The first chapter of the book is devoted to explaining optimal transport from the ground up, starting with the Monge problem.

In the Monge problem, we assume that the cost is proportional to the distance. But there are many different possible cost functions. The most general formulation of Kantorovich’s problem is:

\[\inf_{\gamma \in \Gamma(\mu, \nu)} \int c(x,y) \gamma(dx, dy)\]

where $c$ is the cost function. The Monge problem corresponds to the case when $c(x,y) = | | x - y | |$. One important class of cost functions is $c(x,y) = ||x -y||^p$. The induced distances for these cost functions are called Wasserstein-$p$ metrics. The case that is most studied throughout this book is the Wasserstein-2 metric, corresponding to the cost function: $c(x,y) = ||x-y||^2$.

Another interesting case is the total variation distance. If you imagine two probability distributions as graphs plotted on the same set of axes, the total variation distance measures the area where they do not overlap.

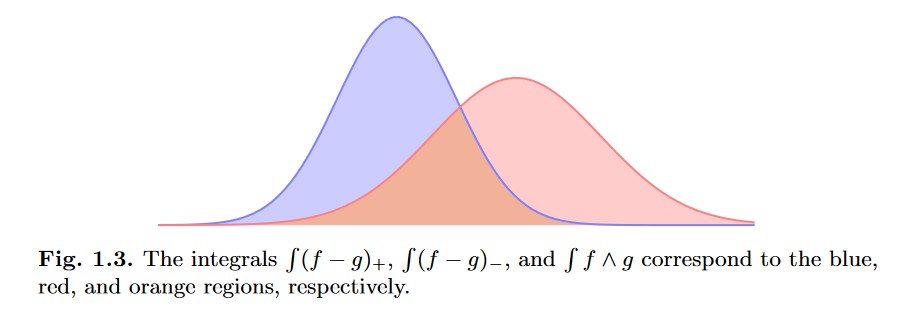
It turns out that the total variation distance is the Wasserstein-0 metric. If your cost function is the indicator function: $c(x,y) = \mathbb{1}_{x \neq y}$ (so there is a cost associated with moving the speck of dirt, but the cost is not sensitive to the distance traveled), then you recover the total variation distance.

A running theme throughout this book is convex optimization. Convex optimization is a subfield of math concerned with optimization problems where the set of objects under consideration is convex. There are multiple equivalent notions of convexity. One definition is that a set is convex if, for any two objects in the set, the object halfway between them is also in the set (what “halfway between” means will depend on the mathematical structure of the set in question).

Optimal transport is a convex optimization problem; the set of couplings $\Gamma(\mu, \nu)$ is convex. If we have $\gamma_1, \gamma_2 \in \Gamma$, then the mixture measure $\gamma = \frac{1}{2}(\gamma_1 + \gamma_2)$ will retain the marginals of $\mu$ and $\nu$ (meaning that $\gamma$ will be in $\Gamma(\mu, \nu)$ as well).

Convex functions also play an important role in one of the crowning jewels of optimal transport theory: Brenier’s theorem. We mentioned before that the strength of Kantorovich’s formulation of the Monge problem is that it doesn’t assume the existence of a transport map (and indeed, one can show that in certain simple cases that no transport map exists).

But if the target measure $\nu$ is absolutely continuous with respect to original measure $\mu$, then a transport map does exist.

\[T_{\#}\mu = \nu\]

where the expression above should be read as “$\nu$ is the pushforward measure of $\mu$ acted on by $T$”.

Brenier’s theorem says that this transport map must be the gradient of some convex function $\phi$. And this is an if and only if: if there is a transport map $T$ which pushforwards $\mu$ to $\nu$ and $T$ is the gradient of a convex function, the optimal coupling must correspond to the law of $(X, T(X))$ where $X \sim \mu$.

The intuitive idea behind Brenier’s theorem is that gradients of convex functions are the natural generalization of monotonic functions from one dimension to higher dimensions. If you consider the transport problem in one dimension, our intuition tells us that a transport plan where two specks of dirt cross each other would be sub-optimal. So if you have two specks of dirt, one located at $x=a$ and the other located at $x =b$, then if $a < b$ and $T$ is the optimal transport map, we should have that $T(a) < T(b)$. This is precisely the definition of monotonicity.

But notice that, in one dimension, the antiderivative of a monotonic function is a convex function (from which it follows that the derivative of a convex function is a monotonic function). So when we want to move to higher dimensions (which aren’t totally ordered spaces like the case when you have only one dimension), we replace the monotonicity condition with the condition that the transport map $T$ must be the gradient of some convex function $\phi$.

Convex optimization also plays an important role in the dual formulation of the optimal transport problem. Rather than searching for the optimal coupling which minimizes the overall cost, one can instead search for the pair of functions $f$ and $g$ such that their expectation with respect to $\mu$ and $\nu$, respectively, are maximized. $\Big ($With the constraint that $f(x) + g(y) \le c(x,y)$. $\Big )$ $f$ and $g$ are called the Kantorovich potentials.

To show that the two formulations are equivalent is not too complicated, but I will still elide the proof. The original version in terms of optimal couplings is called the primal problem. The alternative formulation in terms of optimal functions is called the dual problem.

So we have two ways of understanding the Wasserstein distance. We can then ask: how do we go about estimating the Wasserstein distance between two probability measures?

Unfortunately, to estimate the Wasserstein distance involves a lot of fussy proofs using dyadic cubes. These types of proofs bored me when I was first exposed to measure theory and still bore me now.

The Wasserstein distance gives an interesting perspective on a phenomenom called the curse of dimensionality. The curse of dimensionality is a broad term that encompasses all the different ways that our low-dimensionally-adapted intuitions break down when working in higher-dimensions. We mentioned before that the standard deviation of the mean behaves asymptotically with respect to sample size $n$ as $\frac{1}{\sqrt{n}}$. But in settings like machine learning or genomics—spaces where the data is extremely high-dimensional—we also care about the asymptotic behavior of statistical estimators as a function of the number of dimensions $d$ of the underlying data space. And it turns out that a lot of classical statistical estimators break down in higher-dimensions.

Let’s revisit our example of the standard deviation of the mean, but for simplicity, restrict ourselves to the problem of of estimating the mean of a $d$-dimensional Gaussian which is the product distribution of uncorrelated uni-dimensional Gaussians of unit variance.

\[\prod_{i=1}^d \frac{1}{\sqrt{2\pi}} e^{-\frac{(x_i - \mu_i)^2}{2}} = \frac{1}{(2\pi)^{d/2}} e^{-\frac{1}{2}\sum_{i=1}^d (x_i - \mu_i)^2}\]

We are interested in two questions:

1. Keeping the sample size $n$ fixed, what is the asymptotic relationship between the SEM and the number of dimensions $d$?
2. Keeping the number of dimensions $d$ fixed, what is the asymptotic relationship between the SEM and the sample size $n$?

It turns out that we have the following relation for the SEM:

\[\text{SEM} \propto \sqrt{\frac{d}{n}}\]

So we have that the SEM goes as $\sqrt{d}$. To see why that would be the case, consider the random variable $R^2$ which is squared distance of the SEM from the true mean:

\[R^2 = \sum_{i=1}^d (\bar{X_i} - \mu_i)\]

where $\bar{X_i}$ is the sample mean of $i$-th component of the sample. Because (by assumption) we have that ${X_i}$ are independent, the expectation of $R^2$ should be linear in $d$. So the expectation of $R$ (the absolute distance of the sample mean to the population mean) should go as $\sqrt{d}$.

Notice that, keeping the number of dimensions fixed, the SEM still goes asymptotically as $\frac{1}{\sqrt{n}}$—the same as in the one-dimensional case. This is a powerful result. For the SEM, the dimension-dependence appears as a pre-factor, but the overall scaling law of $n$ remains unchanged. This is sometimes included as an implication of the law of large numbers.

But what about the Wasserstein distance between the empirical distribution and true distribution? Does the Wasserstein distance exhibit similar scaling relationships in $d$ and $n$ as the SEM?

No. For the Wasserstein distance, the scaling relationships are more complicated:

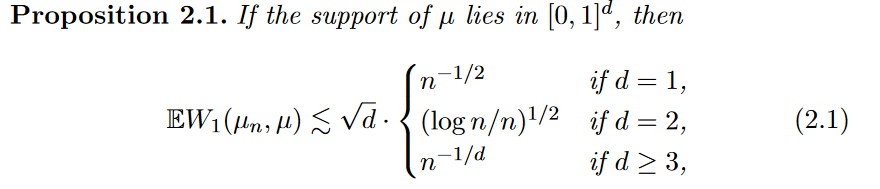
We won’t dwell on the details (like the particularly interesting case when $d = 2$). But the key point is that, in the case of SEM, the assympotic behavior of $n$ is independent of the dimension $d$. But for the case of the Wasserstein distance, we have a $d$-dependence on the assymptotic behavior: the larger that $d$ is, the slower our empirical distribution is to converge in Wasserstein distance to our true distribution. For even a moderate number of dimensions (e.g. a thousand dimensions), the convergence rate is unacceptably slow.

This is the curse of dimensionality.

The remaining chapters on optimal transport theory concern estimating transfer maps and entropic optimal transport (optimal transport but with an added regularization term that penalizes low-entropy couplings).

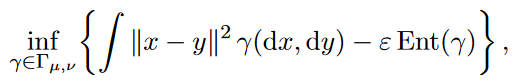
Both are interesting topics. What they have in common is that they both lean heavily on the dual formulation.

For transfer maps, a common problem arises when we attempt to estimate the optimal transfer map $T$ from $\mu$ to $\nu$ by constructing the optimal transfer map between their corresponding empirical distributions: $\hat{T}$ from $\mu_n$ to $\nu_n$. The key difficulty is determining how to extrapolate in a principled way to data points that weren’t sampled. The general approach is to impose ‘smoothness’ conditions, where the notion of smoothness depends on your structural assumptions. This approach is most elegantly achieved in the dual formulation, as imposing smoothness conditions on the admissible Kantorovich potentials $f$ and $g$ naturally endows the induced transfer map with the desired smoothness properties.

For entropic optimal transport, we turn the constraint of the unregularized dual problem (that $f(x) + g(y) \le c(x,y)$) into an additional term to be optimized (which in the limit as $\epsilon \rightarrow 0$ recovers our original constraint).

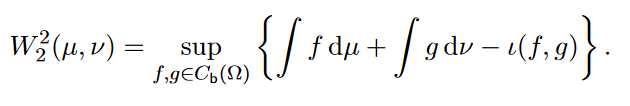
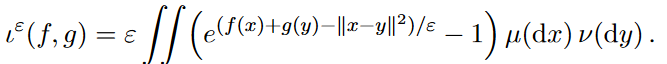
Wasserstein Gradient Flows and Wasserstein Geometry

While the sections on optimal transport are excellent, the beating heart of the book is certainly the back half on Wasserstein gradient flows and metric geometry in Wasserstein space. The key idea (that it shares in overlap with information geometry—but is executed much better in the case of Wasserstein geometry) is that when equipped with the Wasserstein distance, the space of probability measures form a metric space. This allows us to use tools from Riemannian geometry to understand our space of probability measures.

Actually making this technically precise is difficult. In contrast with information geometry which uses the Fisher information as the metric tensor as the jumping off point for the theory, the Wasserstein distance is not a local tensoral object but a global metric on the entire space. “Localizing” the Wasserstein distance properly requires a bit of technical exposition that the book prefers to elide (it cites Gradient Flow by Ambrosio as the go-to resource to seeing the Riemmanian picture of optimal transport made precise).

To understand Wasserstein gradient flow, it helps to review normal gradient flow.

Imagine you have a ball trapped inside of a valley. And for simplicity, suppose that the mass of the ball and the coefficient of friction are such that the ball is always at travelling at terminal velocity: the instantaneous velocity of the ball is solely determined by its location in the valley, independent of its past history. (We could say the the ball is living life at low Reynolds number.)

We know that balls roll downhill. But why? Because objects “want” to minimize their gravitational potential energy. But it’s not just that the ball will tend to go downhill over time. The implication is much stronger than that: at any given moment in time, if the ball isn’t being acted on by any other forces, the ball will be travelling precisely in the direction of steepest descent—the direction that minimizes its potential energy as quickly as possible. The direction of the steepest descent can be found by taking the gradient of the gravitational potential. We can then determine the dynamics of the ball by representing the gradient at each point in space as a vector field and moving the ball in accordance with this vector field. This is gradient flow.

Just like how balls roll downhill, the evolution of a probability measure over time can be visualized as the probability measure “rolling down hill”, as determined by the potential landscape given by some functional. This was most famously explained in a landmark paper ‘The Variational Formulation of the Fokker–Planck Equation’ (JKO 1998), where they showed the Fokker-Plank equation can be reinterpreted as defining a gradient flow in the space of probability measures. Here, the potential is $\text{KL}(\mu_t, \pi)$ where $\pi$ is the stationary distribution of our Fokker-Plank equation.

What’s the connection with Wasserstein geometry? The direction of steepest descent is the direction which has the largest decrease in the potential per unit length. But for this to make sense, we need a notion of distance between probability measures.

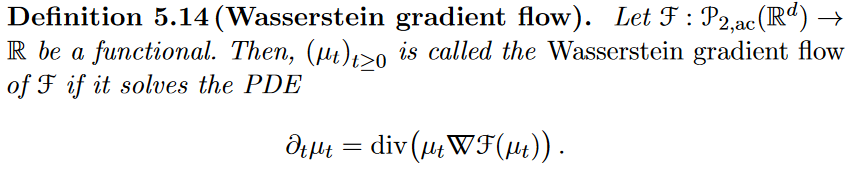
It turns out that the Wasserstein-2 distance is precisely the right notion of distance with which to understand Wasserstein gradient flow.

Wasserstein Barycenters

The last chapter is on Wasserstein barycenters. Barycenters are generalizations of the mean to spaces where there isn’t a well-defined notion of addition. In Euclidean space, the mean has the property that, given a set of points $x_i$, it minimizes the functional

\[D(\mu) = \sum_i^n d^2(x_i, \mu)\]

where $d^2(\cdot, \cdot)$ is the Euclidean metric squared. This definition can be generalized to other metric spaces: the center of a cluster of points is the point which is the least far from all of them simultaneously.

This idea of a barycenter becomes interesting when considering more abstract spaces than Euclidean space. For example, consider the space of images. We can represent images with $d$ pixels arranged in a square grid, with three colors channels per pixel (so the overall space is encoded in $\mathbb{R}^{3d}$).

But you could ask: given two images, what’s the “average” of the two images? The naive way of doing it—averaging the pixel intensities—isn’t the correct approach. But why not?

The short answer: Because our embedding from the abstract space of images to their representations in pixels isn’t an isometry.

To elaborate: You can imagine that images live in some abstract space where images are close to each other if they are semantically similar. Two images are semantically similar if they represent the same underlying concept(s). There is no reason a priori why the semantic distance between abstract images would match the Euclidean distance between their embedded representation as pixels in $\mathbb{R}^{3d}$.

This motivating example was interesting enough that I wanted to include it. I think a lot about semantic structure of language, especially in the context of machine learning. But I notice (unless I missed it during my re-reading) that the book never answers how one would go about finding the semantic distance between images. But I guess that’s a rich topic better suited for a different book.