What is Information Geometry?
Information Geometry is a niche subfield of mathematics that uses the tools of differential geometry to study parametric families of probability distributions. The key insight is that parametric families of probability distributions have a natural manifold structure. The manifold (called the statistical manifold) is such that each point on the manifold is a probability distribution in the parametric family and the coordinates of the manifold are given by the parameter values corresponding to that probability distribution.
Consider the parametric family of normal distributions. It forms a two-dimensional statistical manifold. While there are many ways that we can parametrize the family of normal distributions, one canonical choice is to choose as coordinates the mean $\mu$ and the variance $\sigma^2$.
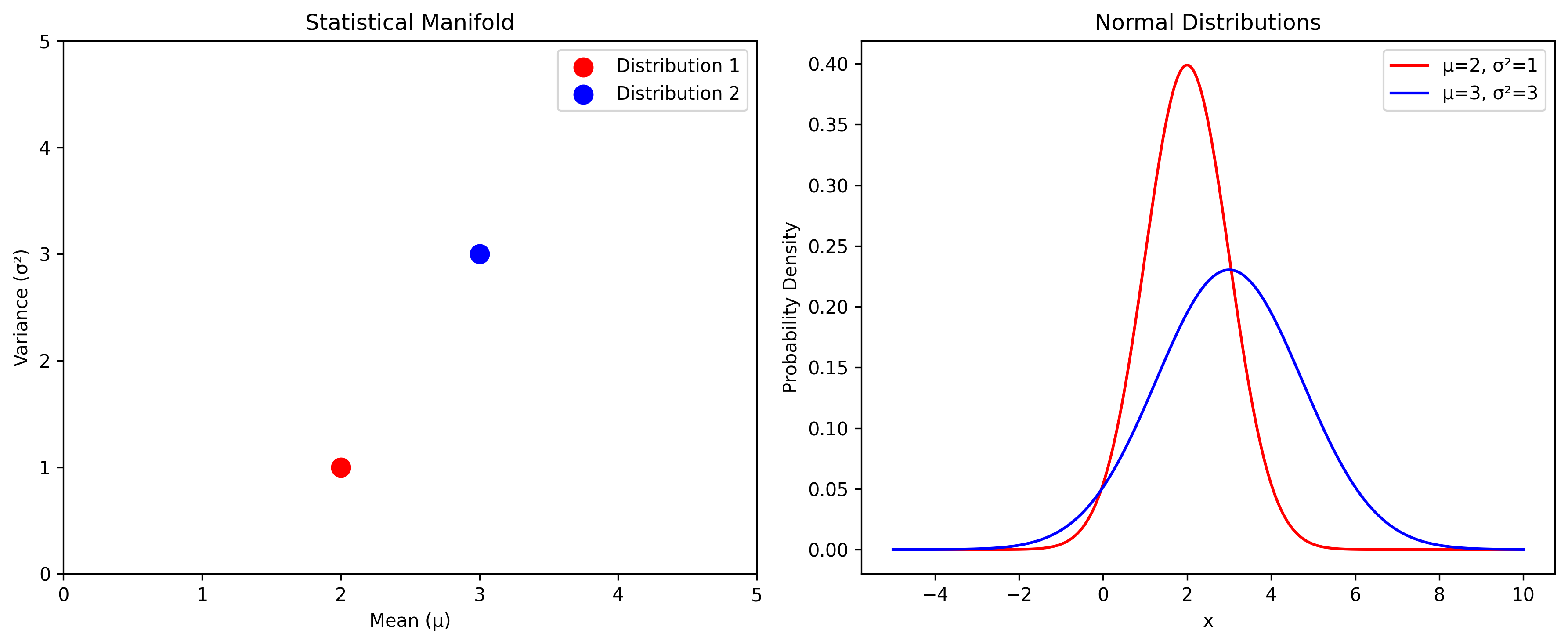
In the image above, we have on the left a coordinate chart with two colored dots corresponding to two different normal distributions with differing values for their mean and variance. On the right, we plotted the probability density functions for each of the distributions on the same set of coordinate axes. If you imagine extending our coordinate chart to the entire half-plane ($- \infty < \mu < \infty$;$0 < \sigma^2 < \infty$), we would be able to represent every (non-degenerate) normal distribution on the statistical manifold.
While we can use the Euclidean half-plane as the coordinate chart of our statistical manifolds of normal distributions, the two spaces are not “strongly” isomorphic. In mathematics, there are different notions of isomorphic—with some notions being stronger than others. For example, the real numbers $\mathbb{R}$ and the complex numbers $\mathbb{C}$ are isomorphic as sets (they both have the cardinality of the continuum), but they aren’t isomorphic algebraicly or topologically. Here, we have that our statistical manifold is isomorphic to the Euclidean half-plane both as a set and as a topological space, but not geometrically. The statistical manifold of normal distributions differs from the Euclidean half-plane in terms of distances between points, the angles at which curves intersect, and the intrinsic “curvature” of the space.
Indeed, this is the whole point of why we study manifolds in the first place: Manifolds are locally Euclidean spaces. Similar to how a circle locally looks like a line and a sphere locally looks like a plane, while the global structure of the manifold can be rich, in the neighbourhood of a given point, it looks an $n$-dimensional Euclidean space.
The father of Information Geometry is Japanese mathematician Shun-ichi Amari. He first started working on Information Geometry in the late 1960s, and really started developing the foundations of the field in earnest in the 70s. While Amari is certainly the most important figure in the field, the roots of Information Geometry are older, going all the way back to the work of C.R. Rao who noticed that the Fisher Information could be interpreted as a Riemannian metric.
The core insight of Information Geometry is that while parametric families admit many different parameterizations, the relationship between the various probability distributions in the family should be independent of the specific parametrization that is chosen. Information geometers work to develop tools to elucidate that fundamental structure of the space.
While Information Geometry is interesting, it’s niche and hasn’t been as successful as a research program as its proponents in the 70s would have hoped. Why Information Geometry “failed” is an interesting question that I am looking to understand better.