The Ap Distribution
E.T. Jaynes introduces this really interesting concept called the $A_p$ distribution in his book Probability Theory. Despite the book enjoying a cult following, the $A_p$ distribution has failed to become widely-known among aspiring probability theorists. After finishing the relevant chapter in the book, I googled the phrase “Ap distribution” in an attempt to learn more, but I didn’t get many search results. So here’s an attempt to explain it for a wider audience.
The $A_p$ distribution is a way to give a probability about a probability. It concerns a very special set of propositions ${A_p}$ that serve as basis functions for our belief state about a proposition $A$—somewhat similarly to how the Dirac delta functions can serve as basis elements for measures over the real line. The proposition $A_p$ says that “regardless of whatever additional evidence that I’ve observed, the probability that I will assign to proposition $A$ is $p$”. It’s defined by the rule:
\[P(A|A_p E) = p\]This is a fairly strange proposition. But it’s useful as it allows us to encode a belief about a belief. Here’s why it’s a useful conceptual tool:
If we say that there is a $1/2$ probability of some proposition $A$ being true, that can represent very different epistemic states. We can be more or less certain that the probability is “really” $1/2$.
For example, imagine that you know for sure that a coin is fair: that in the long run, the number of heads flipped will equal the number of tails flipped. Let $A$ be the proposition “the next time I flip this coin, it will come up heads.” Then your best guess for $A$ is $1/2$. And importantly, no matter what sequence of coin flips you observe, you will always guess that there is a 50% chance that the next coin flip lands on heads.
But imagine a different scenario where you haven’t seen a coin get flipped yet, but you are told that it’s perfectly biased towards either heads or tails. Because of the principle of indifference, we would assign a probability of $1/2$ to the next coin flip landing on heads—but it’s a very different $1/2$ from the case when we had a fair coin. Just one single flip of the coin is enough to collapse the probability of $A$ to either $p = 0$ or $p =1$ for all time.
There is a useful law in probability called the law of total expectation. It says that your expectation for your future expectation should match your current expectation. So given a static coin, the probability that you give for the next coin flip being heads should be the same as the probability that you give for 100th or 1000000th coin flip being heads.
Mathematically, the law of total expectation can be expressed as:
\[E[X] = E[E[X|Y]]\]The law of total expectation is sometimes bastardized as saying “you shouldn’t expect your beliefs to change.” But that’s not what it’s saying at all! It’s saying that you shouldn’t expect your expectation—the center of mass of your state of belief—to change. But all higher moments in belief space can and do change as you acquire more evidence.
And this makes sense. Information is the opposite of entropy; if entropy measures our uncertainty, than information is a measure of our certainty: how constrained the possible worlds are. If I have a biased coin, I give a 50% chance that the 100th flip lands on heads. But I know now that right before the 100th flip, I will be in an epistemic state of 100% certainty in the outcome—it’s just that current me doesn’t know what outcome future me will be 100% certain in.
A way to think about the proposition $A_p$ is as a kind of limit. When we have little evidence, each bit of evidence has a potentially big impact on our overall probability of a given proposition. But each incremental bit of evidence shifts our beliefs less and less. The proposition $A_p$ can be thought of a shorthand for an infinite collection of evidences ${F_i}$ where the collection leads to an overall probability of $p$ given to $A$. This would perhaps explains why the $A_p$ proposition is so strange: we have well-developed intuitions for how “finite” propositions interact, but the characteristic absorbing property of the $A_p$ distribution is more reminiscent of how an infinite object interacts with finite objects.
For any proposition $A$, the probability of $A$ can be found by integrating over our probabilities of ${A_p}$
\[p(A) = \int_{0}^{1} dp \ p(A_p)\]where $p(A_p)$ can be said to represent “the probability that, after encountering an infinite amount of evidence, I will give a probability of $p$ to the proposition $A$.”
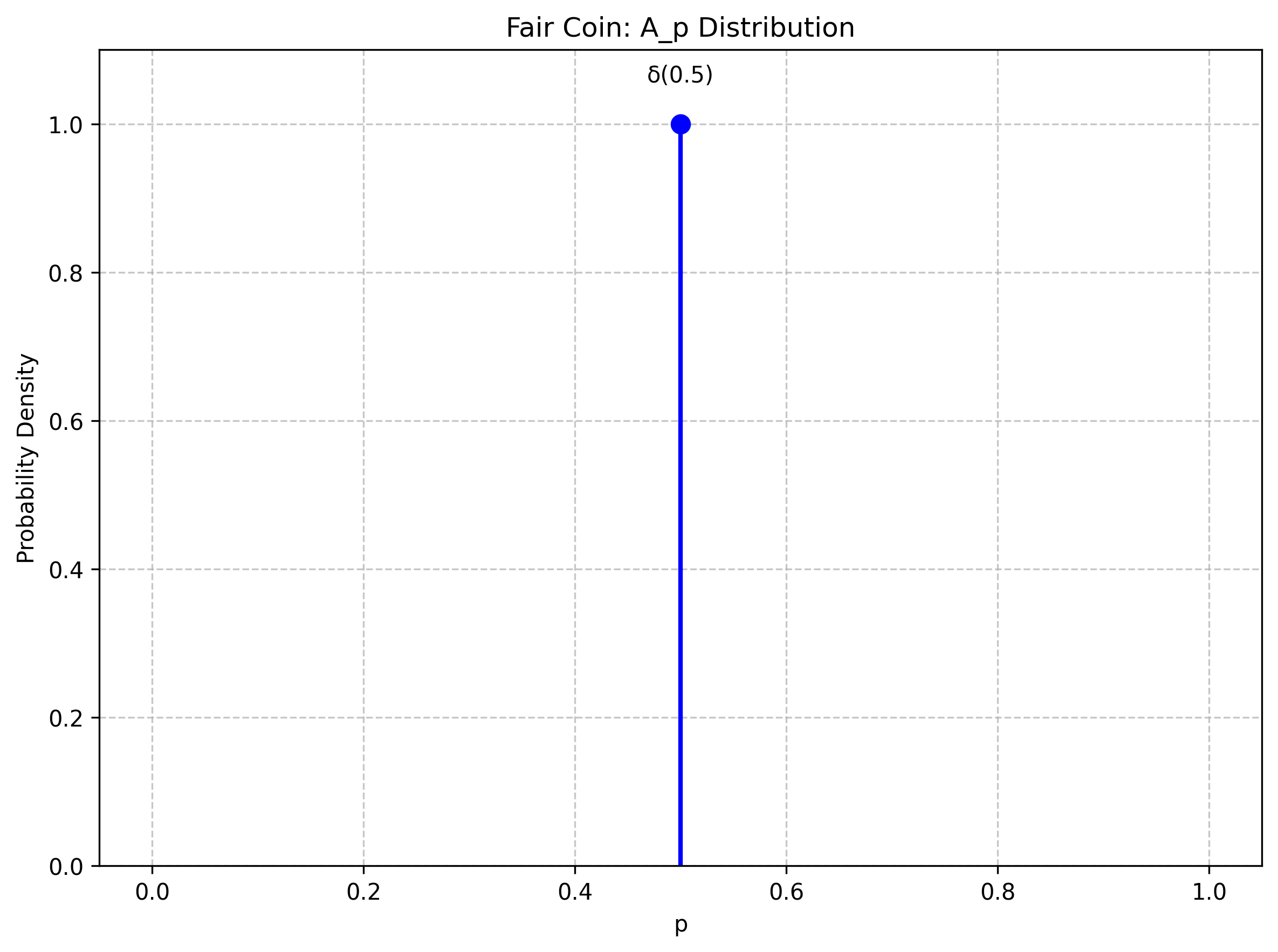
For the fair coin, our belief in $A_p$ space would be represented by a delta function at $p=1/2$.
For the biased coin (where we don’t know the bias), our belief would be represented by two deltas of weight 1/2 at $p=0$ and $p=1$.
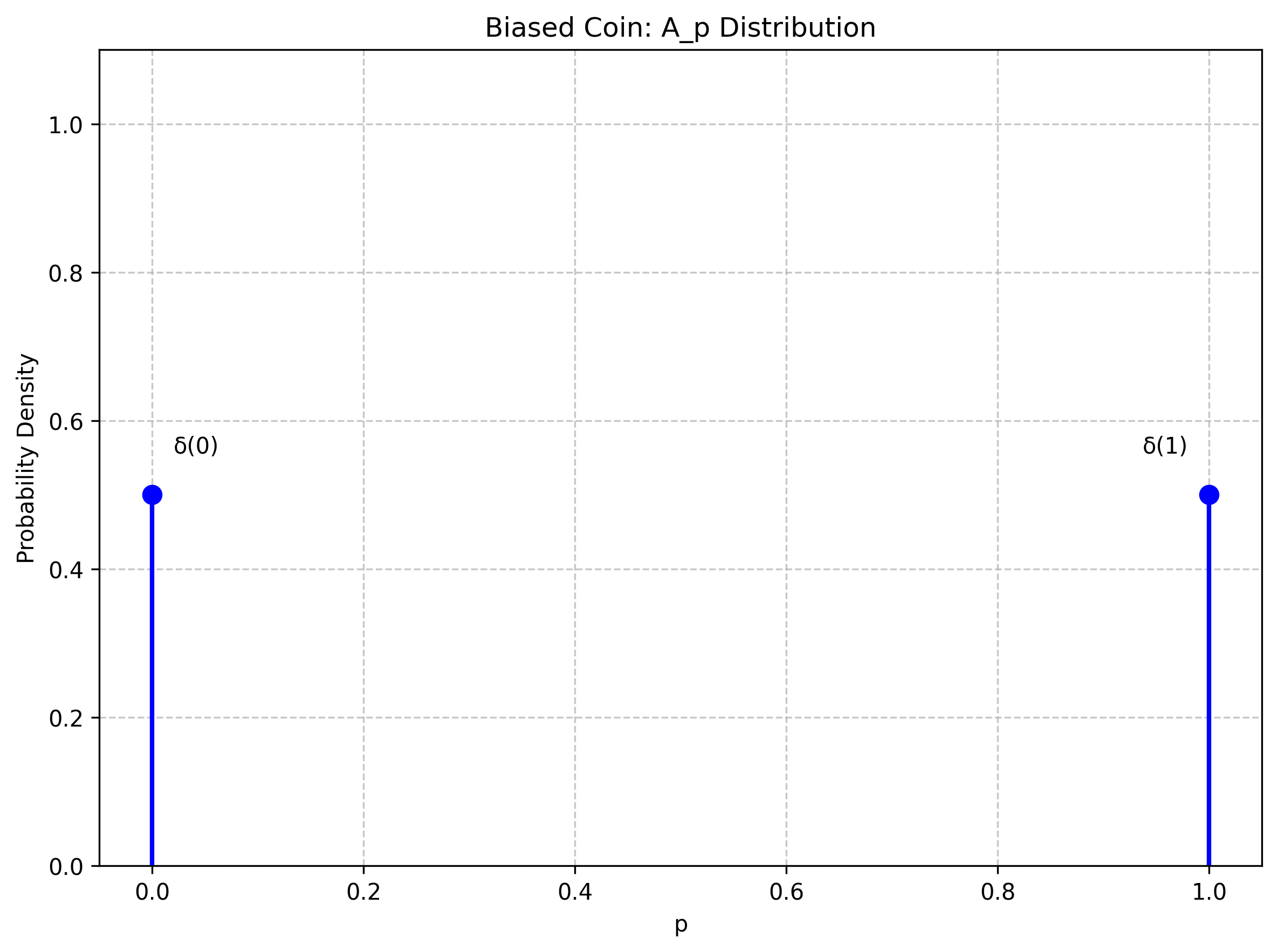
Both distributions assign a probability of $1/2$ to $A$. But the two distributions greatly differ in their variance in $A_p$ space.